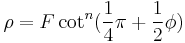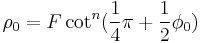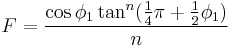Lambert conformal conic projection

A Lambert conformal conic projection (LCC) is a conic map projection, which is often used for aeronautical charts. In essence, the projection seats a cone over the sphere of the Earth and projects conformally onto the cone. The cone is unrolled, and the parallel touching the sphere is assigned unitary scale in the simple case. This parallel is called the reference parallel or standard parallel.

By scaling the resulting map, two parallels can be assigned unitary scale, with scale decreasing between the two parallels and increasing outside them. This gives the map two standard parallels. In this way, deviation from unitary scale can be minimized within a region of interest bounded by two parallels somewhat outside of the two standard parallels. Unlike other conic projections, no true secant form of the projection exists because using a secant cone does not yield the same scale along both standard parallels.[1]

Pilots favor these charts because a straight line drawn on a Lambert conformal conic projection approximates a great-circle route between endpoints as long as distances are not great. The European Environment Agency recommends its usage for conformal pan-European mapping at scales smaller or equal to 1:500,000.[2]

In the United States, the National Geodetic Survey's "State Plane Coordinate System of 1983" uses Lambert Conformal Conic Projection to define the grid-coordinate systems used in several States (primarily those that are elongated west to east, like Tennessee). The Lambert projection is relatively easy to use: conversions from Geodetic (latitude/longitude) to State Plane Grid coordinates involve trigonometric equations that are fairly straightforward and which can be solved on most scientific calculators, especially programmable models.[3] Lambert projection as used in CCS83 yields maps in which scale errors are limited to 1 part in 10,000.

Contents

History

The Lambert conformal conic is one of several map projection systems developed by Johann Heinrich Lambert, an 18th century Swiss mathematician, physicist, philosopher, and astronomer.

Transformation

Coordinates from a spherical datum can be transformed into Lambert conformal conic projection coordinates with the following formulas,[4] where λ is the longitude, λ0 the reference longitude, φ the latitude, φ0 the reference latitude, and φ1 and φ2 the standard parallels:

x = \rho \sin[n (\lambda - \lambda_0)]
y = \rho_0 - \rho \cos[n (\lambda - \lambda_0)]

where

n = \frac{\ln(\cos \phi_1 \sec \phi_2)}{\ln [\tan (\frac14 \pi %2B \frac12 \phi_2) \cot (\frac14 \pi %2B \frac12\phi_1)]}
\rho = F \cot^{n} (\frac14 \pi %2B \frac12 \phi)
\rho_0 = F \cot^{n} (\frac14 \pi %2B \frac12 \phi_0)
F = \frac{\cos \phi_1 \tan^{n} (\frac14 \pi %2B \frac12 \phi_1)}{n}

Formulæ for ellipsoidal datums are more involved.

See also

References

  1. ^ "CMAPF FAQ". NOAA. http://www.arl.noaa.gov/faq_ms1.php#Q8. 
  2. ^ "Short Proceedings of the 1st European Workshop on Reference Grids, Ispra, 27-29 October 2003". European Environment Agency. 2004-06-14. p. 6. http://eusoils.jrc.ec.europa.eu/Projects/Alpsis/Docs/ref_grid_sh_proc_draft.pdf. Retrieved 2009-08-27. 
  3. ^ "State Plane Coordinate System of 1983, NOAA Manual NOS NGS 5". National Oceanic and Atmospheric Administration. 1990-03. http://www.ngs.noaa.gov/PUBS_LIB/ManualNOSNGS5.pdf. Retrieved 2011-10-27. 
  4. ^ Weisstein, Eric. "Lambert Conformal Conic Projection". Wolfram MathWorld. Wolfram Research. http://mathworld.wolfram.com/LambertConformalConicProjection.html. Retrieved 2009-02-07. 

External links